동적 계획법 DP(Dynamic Programming)은 하나의 큰 문제를 여러 개의 작은 문제로 나누어서 그 결과를 저장하여 다시 큰 문제를 해결할 때 사용하는 일종의 문제 해결법으로 볼 수 있습니다. 즉 작은 문제로 쪼개서 답을 저장해두고 이를 재활용하는 기억하며 풀기 방법이라 할 수 있죠. 일반적인 재귀를 사용하면 동일한 문제가 반복 계산되는데, 이를 효율적으로 활용할 수 있어요.

DP가 적용되기 위해서 2가지 조건을 만족해야 합니다.

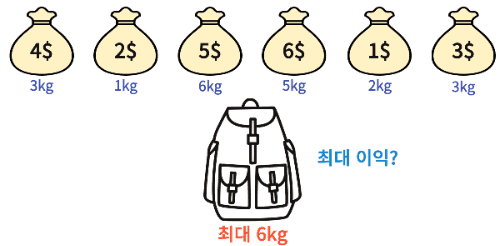
위 그림과 같이 최대 적재량이 존재하는 배낭과 각각 무게와 가치를 가지는 아이템이 존재합니다. 이때 배낭에 들어가는 아이템 가치의 합이 가장 높을 때 값은?

이는 배낭의 최대 용량이 $w$일 때, $i$번째 아이템까지 넣었을 때 최대 가치를 계산하는 방법으로 구현할 수 있다. 위 문제에서 표를 만들어 본다면 아래와 같이 표현할 수 있다.

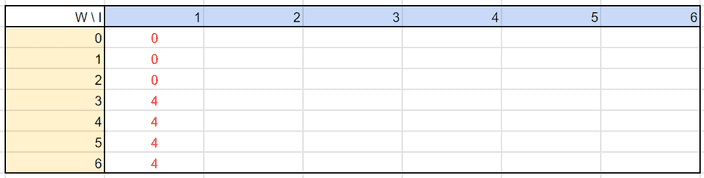
첫 번째 아이템을 넣기 위해 $3kg$ 이상의 공간이 필요합니다. 따라서 $w$가 3이하에서 0의 가치를, $w$가 3이상에서 4의 가치를 가지게 되죠.

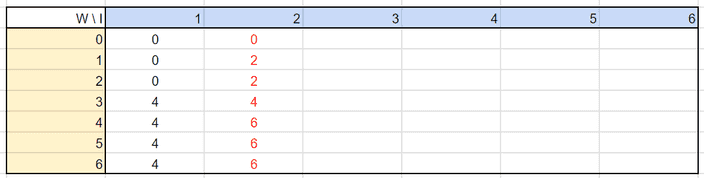
두 번째 아이템을 넣는 경우를 생각해봅시다. $w$가 1, 2일 때 아무 아이템도 들어가지 않았던 첫 번째 순서에 비해 무게가 1인 두 번째 아이템에 경우에는 가방에 들어갈 수 있겠죠.

그러나 $w$가 3일 때 첫 번째 아이템이 들어가있는 경우의 가치가 첫 번째 아이템을 빼고 두 번째 아이템을 넣는 경우보다 더 높습니다. 따라서 이 경우에는 두 번째 아이템을 넣지 않는 것이죠.

$w$가 4이상인 경우, 기존에 들어간 첫 번째 아이템에 추가로 두 번째 아이템을 넣을 수 있습니다.

위 세 가지 경우를 조금 일반화 해볼게요. 위 식 모두는 동일 용량의 직전 아이템까지 넣었을 때 가치와, 새로 들어오는 아이템의 용량만큼 비운 후 새로운 아이템의 가치를 더한 값을 비교해서 더 큰 값을 취한다는 전략을 사용할 수 있을 것입니다.

이를 모든 항에 적용할 수 있도록 일반화한다면

이 식을 이용하여 모든 표를 작성하면 아래와 같은 순서로 완성시킬 수 있겠습니다.

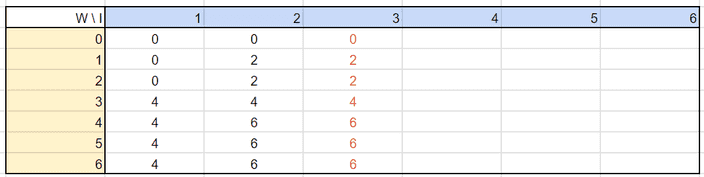
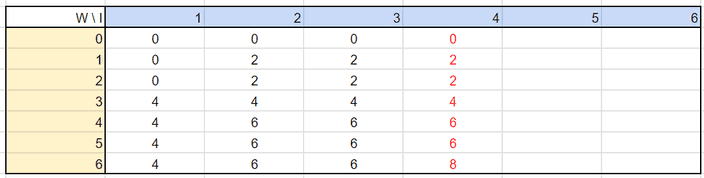
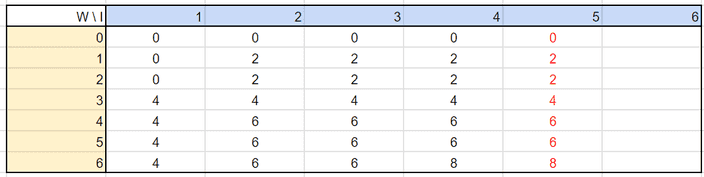
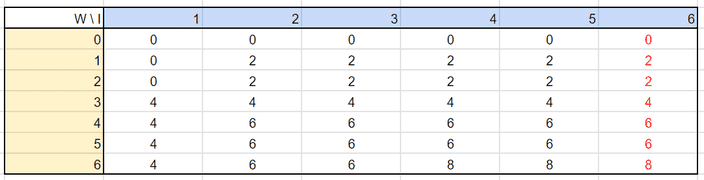
이를 코드로 구현해볼게요.

1

1

1

1

1, 3, 4원짜리 동전이 있을 때, $x$원을 최소한의 동전으로 교환하는 문제

이는 Greedy Algorithm으로 해결한다면 4, 1, 1로 3개의 동전이 필요합니다. 하지만 3, 3으로 2개의 동전만으로도 교환할 수 있죠. 이를 DP로 구현해봅시다.

$f(x)$는 $x$를 교환 가능한 최소한의 동전 수 라고 할 때, 먼저 1, 2, 3, 4에 대해 최적의 방법을 구합니다.

1

이후 $x$를 1씩 원하는 금액에 이를 때까지 증가시킵니다. 이때 이전에 계산한 결과를 이용하는 방식이죠.

1

이렇게 DP를 이용하여 동전 교환 문제를 해결할 수 있습니다.

1